Objetivo de la obra El Mundo de los Niños es para los niños. En esta frase quedó resumido el objetivo...
Viruela, Varicela, Venenos, Verrugas, Virus, Vitaminas, Vómitos, Zumaque
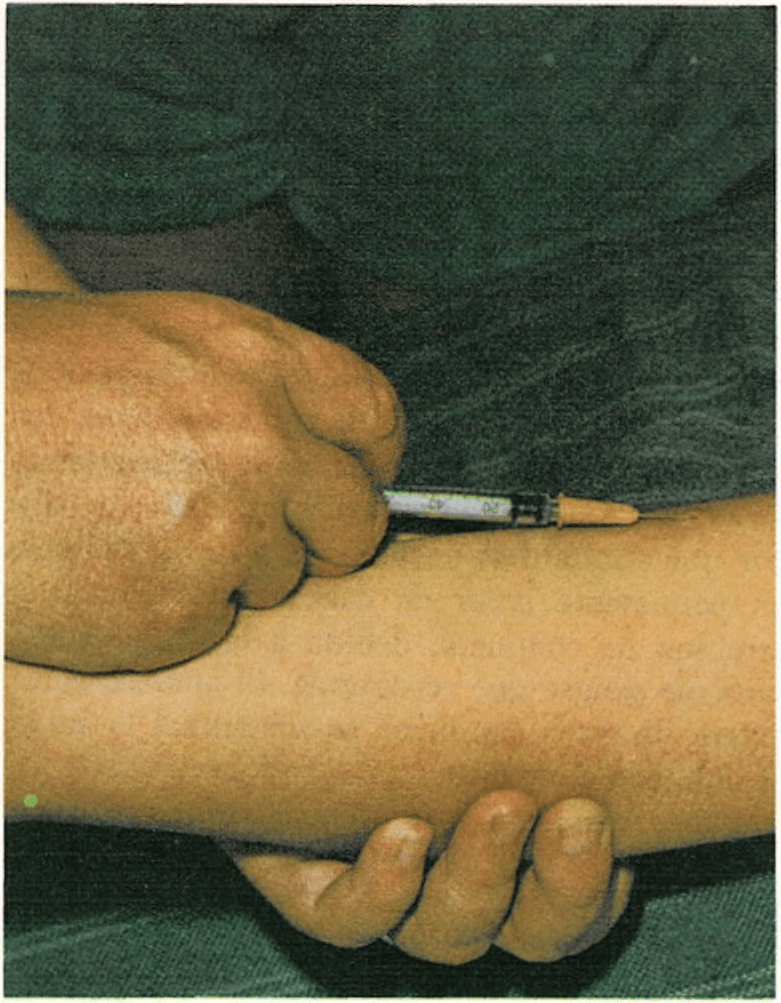
Vacuna de la viruela Esta debería ser inoculada a todos los niños de 1 a 2 años; no obstante el...
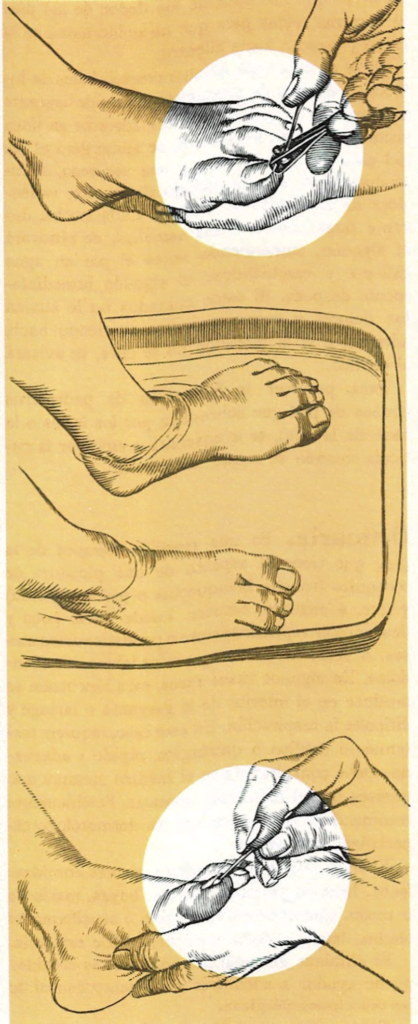
Úlceras bucales, Uñas, Urticaria
Ulceras bucales Son dolorosas, pudiendo formarse una o varias a la vez. Curan por sí mismas en un período de...
Tartamudeo, Testículos, Tétanos, Tics, Tiñas, Tos, Tragarse objetos, Trastornos urinarios, Traumatismos craneales, Tuberculosis
Tartamudeo Es una interrupción en la fluidez del lenguaje causada por la repetición de ciertos sonidos, prolongación de otros y...
Sarampión, Sarpullido, Sepsis, Sinusitis, Soplo cardíaco, Sordera, Sueño, Supositorios
Sarampión Es una enfermedad muy contagiosa causada por un virus. Puede prevenirse mediante la vacunación y la mayoría de los...